Multicomponent reactive transport in natural porous media

Application of our cpu-time saving 'Reduction Scheme' (Richy2D/3D) to the MoMaS Benchmark on Reactive Transport Carbon dioxide storage by mineral trapping

Description / Outline

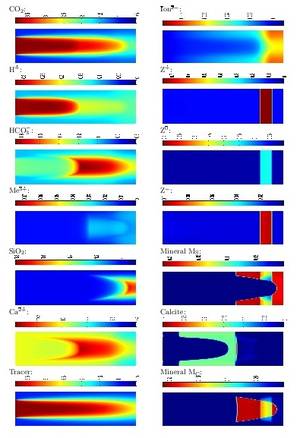
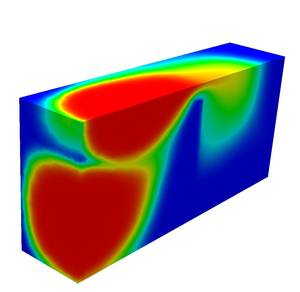
The modeling of reactive transport problems in porous media leads to large systems consisting of partial and ordinary differential equations, coupled through source terms (e.g., arising from kinetic reactions) and through algebraic equations (coming from very fast, i.e., equilibrium reactions). If mineral precipitation-dissolution reactions are involved, then the system is additionally coupled to a complementarity problem.
Our work has the following main foci:
The modelling of the processes (including mineral precipitation-dissolution, electrostatic forces, the influence of microbia), the development of efficient and robust numerical techniques for such systems, and the analysis of such systems, in particular the question of existence of global solutions, which is tackled with fixed point techniques.

Faculty/Institution

Lehrstuhl für Angewandte Mathematik (Modellierung und Numerik)

Contacts

PD Dr. Nadja Ray Naturwissenschaftliche Fakultät, Department Mathematik, Lehrstuhl für Angewandte Mathematik (Modellierung und Numerik), Professur für Visual Computing Tobias Elbinger Lehrstuhl für Angewandte Mathematik (Modellierung und Numerik) Dr. Alexander Prechtel Lehrstuhl für Angewandte Mathematik (Modellierung und Numerik) PD Dr. Raphael Schulz Naturwissenschaftliche Fakultät, Lehrstuhl für Angewandte Mathematik (Modellierung und Numerik) apl. Prof. Dr. Serge Kräutle Naturwissenschaftliche Fakultät, Lehrstuhl für Angewandte Mathematik (Modellierung und Numerik) Prof. Dr. Peter Knabner Naturwissenschaftliche Fakultät, Lehrstuhl für Angewandte Mathematik (Modellierung und Numerik) Dr. Markus Knodel Lehrstuhl für Angewandte Mathematik (Modellierung und Numerik)